高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における r の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. コーシー・シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない!必要条件・十分条件のくすっと笑える判定方法 | ||
| 17. 同じものを含む円順列の考え方 | ||
| 18. f(f(x))=x の形をした関数方程式の取り扱い方 | ||
| 19. パラメータが2次で表された直線の通過領域 | ||
| 20. 四面体の面上及び内部を表すベクトル |

シンプルで一度聞いたら忘れることがほぼない,くすっと笑える必要条件・十分条件の判定方法を紹介します.
16.1 まずは教科書的な説明から
次の問題を考えてみましょう.
Q. x=3 は x2=9 であるための何条件ですか?逆に x2=9 は x=3 であるための何条件でしょう?
教科書には概ね次のように説明されています.
x=3 を満たす x の集合(これを x=3 の真理集合といいます)を P,x2=9 を満たす x の集合を Q とすると,
P={3}
Q={3,−3}
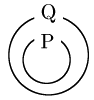
です.2つの集合 P,Q の包含関係は
P⊂Q
となっていて,
命題 「x=3 ⟹ x2=9」⋯(☆)
が真です.このとき
x=3 は x2=9 であるための十分条件
x2=9 は x=3 であるための必要条件
といいます.(☆) の場合,逆の命題すなわち
「x2=9 ⟹ x=3」
は偽です.反例として −3 は2乗すると9になりますが,3ではありません.ですからこのとき
x=3 は x2=9 であるための十分条件ではあるが必要条件ではない.
x2=9 は x=3 であるための必要条件ではあるが十分条件ではない.
という具合に,より詳しく述べることができます.

因みに,x=±3 は x2=9 であるための必要条件であると同時に十分条件でもありますから,このとき,
x=±3 は x2=9 であるための必要十分条件である
といいます.もちろん
x2=9 は x=±3であるための必要十分条件である
もいえます.また
x=±3 と x2=9 は同値である
ともいいます.
このように真理集合の包含関係が次の3つのいずれかのとき,必要条件になったり十分条件になったり,必要十分条件になったりするわけです.
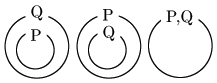
そして次の2つの場合は互いに必要条件にも十分条件にもなりません.
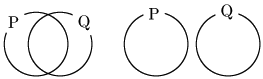

16.2 もう迷わない!必要条件・十分条件の判定方法
教科書的な判定方法ではベン図がなければ判定が難しくなります.「⟹」などの記号表現だけでは「必要」や「十分」といった普段日常で使われる日本語と結びつきにくいからです.そこで,ベン図がなくても判断に困らない秘策を紹介します.
先ほどの x=3 と x2=9 を例に説明します.
x=3 は x2=9 であるための 条件である.
ステップ1 まず双方向に矢印を伸ばします.(図1)

ステップ2 「x=3⟹x2=9」の真偽を判定します.これは真ですから,上側の矢印に○を書きます.逆向きの 「x=3⟸x2=9」は偽でしたから,下側の矢印に×を書きます.(図2)

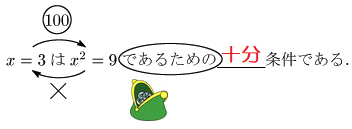
ステップ3 〇の中に「100」を書きます.そして「であるための」を財布だと思います.(図3)
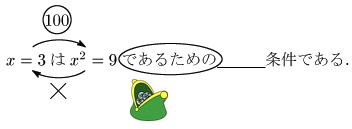
ステップ4 すると,100円玉が財布の中に転がり込んでくる絵になっていますね.お金が財布に入ると「十分」気分が良いので「十分条件」であると判定します.(図4)
それでは次に
x2=9 は x=3 であるための 条件である.
を考えてみます.同じように矢印を伸ばして正しければ○,正しくないならば×を書きます.(図5)

〇の中に100を書き込んで,「であるための」を財布だすると,今度はお金が財布から出ていく絵となっています.(図6)

何か「必要」なものを買うとき,お金が財布から出ていきますから「必要条件」であると判定します.(図7)

最後に
x=±3 は x2=9 であるための 条件である.
を考えます.これはお金が財布に入ると同時に出ていっていますから「必要十分」条件と判定します.(図8)

いかがでしたか?この判定方法だとわざわざベン図を書かなくても必要条件・十分条件を間違えません.是非ほかの問題でも試してみてください!
補足
「であるための」を財布としたのは次のような表現があるためです.
x=3 であるための 条件は x2=9 である.
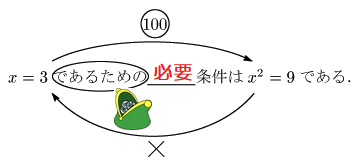
「であるための(財布)」からお金が出ていっていますから「必要」条件です.
このように「右矢印が○なら十分条件だ」と覚えていると,結果が逆になることもあるので,「であるための」が財布だ,という気持ちを忘れないようにしましょう.

16.3 おわりに
この判定方法は,筆者が高校時代に教わった数学の先生から教えて頂いた方法です.当時先生は華頂短期大学の教員もされていたと記憶しています.大学受験時はもちろん,大学に入って専門的な数学を学ぶ時においてさえもこの判定方法に助けられました.ここに先生への心からの感謝の意を記します.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における r の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. コーシー・シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない!必要条件・十分条件のくすっと笑える判定方法 | ||
| 17. 同じものを含む円順列の考え方 | ||
| 18. f(f(x))=x の形をした関数方程式の取り扱い方 | ||
| 19. パラメータが2次で表された直線の通過領域 | ||
| 20. 四面体の面上及び内部を表すベクトル |
