高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |

3.逆関数の微分法
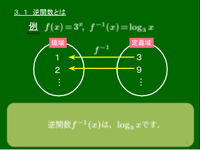
3.1 逆関数とは
まずは関数の復習から
逆関数を論じる前に,「逆」の文字のない通常の「関数」とは何であったかを確認しておこう.
「y は x の関数である」とは
x の値に対して y の値がただ1つ決まるとき, y は x の関数であるという
例として y=x+1 を考える.この式から,
x=0 のとき,y=1
x=1 のとき,y=2
x=2 のとき,y=3
⋮
のように,x の値に対して y の値がただ1つ対応しているから y は x の関数であるといえる.
次に逆の対応を考える
いま x の方を先に決めて,それに応じて y の値が1つ決まったが,逆に y の方を先に決めてもそれに応じて x の値がただ1つ決まる:
y=1 のとき,x=0
y=2 のとき,x=1
y=3 のとき,x=2
⋮
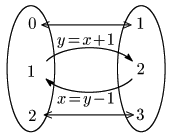
つまり, x は y の関数となっているのである.この逆対応は x=y−1 である.数学においてはしばしば先に決める方の文字を x,それに伴って決まる方の文字を y とおくので,この逆対応を表す関数は x と y の文字を入れ替えて
x=y−1 → y=x−1
と表される.この関数 y=x−1 をもとの関数 y=x+1 の逆関数(inverse function)という.
逆関数とは
関数 y=f(x) について,y の値を先に決めたときにもそれに応じて x の値がただ1つ決まるとする.このとき,x と y を入れ替えた式 x=f(y) を y について解いたときの x の式を関数 f(x) の逆関数といい,f−1(x) で表す.
「f−1(x)」は「f インバース x」と読まれることが多い.
上の例では f(x)=x+1 とすると,f−1(x)=x−1 である.
例
関数 y=2x の逆関数
x=2y を y について解いた y=12x
関数 y=ex の逆関数
x=ey を y について解いた y=logx
注意
逆関数は存在するとは限らない
注意点として,ある関数に対してその逆関数は常に存在するとは限らない.例えば, 関数 y=x2 は x=2 に対して y=4 が対応するが,逆に y=4 のとき, x は 2 と −2 の2つが対応しているため関数とはいえない.つまり関数 y=x2 の逆関数は存在しない.x と y に1対1の対応づけができないからだ.
尚,関数が連続の場合,逆関数が存在しているということは,つまりその関数に単調性があるということである.先ほど関数 y=x2 には逆関数がないと言ったが,例えば定義域を x≧0 に制限してやれば,そこには単調性があるため逆関数 y=√x を考えることができる.
逆関数の逆関数は元の関数である
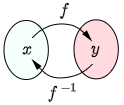
「f(x) の逆関数 f−1(x)」の逆関数は,元の関数 f(x) である.これは f(x) と f−1(x) がそれぞれの逆対応を与えているのだから当然である.f(x) と f−1(x) は互いに逆関数の関係なのだ.
ある関数とその逆関数のグラフは直線 y=x に関して対称
すぐ上の例 からわかるように,ある関数の逆関数を得るには,元の関数の x と y を入れ替えればよい.この操作はグラフを直線 y=x に関して対称移動する際に行う作業に他ならない.従って元の関数と逆関数のグラフは直線 y=x に関して対称である.
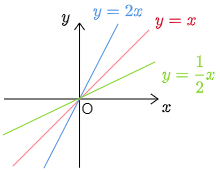
直線 y=x に関して対称
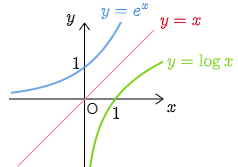
y=ex と y=logx のグラフは
直線 y=x に関して対称

3.2 逆関数の微分法
一見すると微分できそうにない関数
y=sinx という関数は,単調な関数ではないので逆関数は存在しないが,定義域を例えば −π2<x<π2 に制限すれば,この区間内では単調性をもつから逆関数を考えることができる.
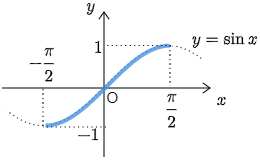
x と y の対応は1対1である.
逆関数は x と y を入れ替えた次に式
x=siny
を y について解いたものである.
さてこの逆関数について y を x で微分するにはどうしたらよいであろうか.この関数を y について解いて y=(x の式)という形にすることはできないし,かと言ってこの形のままではどうすることもできない.
微分したいのに微分できない,でも逆関数の方なら微分できる.そんな時に活躍するのが逆関数の微分法
関数 y=f(x) を微分するのに,この関数の逆関数を利用しようというのがここでの目的である.すぐ上の例でいうと,x=siny という関数の dydx を知るのに,この関数の逆関数,すなわち元の y=sinx の導関数である cosx を利用することができるというのである.
※この問題の解説は 演習問題 参照
逆関数の微分法
それではいよいよ逆関数の導関数を利用した微分法を導出していこう.

関数 y=f(x) について,
y=f(x)⟺f−1(y)=x⋯①
の関係が成り立つ.①の両辺を x で微分すると,
ddxf−1(y)=1⋯②
合成関数の導関数 により,
②の左辺=ddyf−1(y)⋅dydx=dxdy⋅dydx (∵①)
よって,②はdxdy⋅dydx=1 両辺を dxdy で割ってdydx=1dxdy
この最後の dxdy というのが,y=f(x) の逆関数 x=f−1(y) の導関数である.
逆関数の微分法
dydx=1dxdy
例題 x>0 とする.y=x1n (n は自然数)のとき,dydx を求めよ.
こたえ
解答例を表示する
この例題の結果を用いて,以下の公式が示される:
公式 r が有理数のとき, (xr)′=rxr−1
証明
r=mn (m は整数,n は自然数)とおくと, y=xmn=(x1n)m よって合成関数の導関数により, dydx=m(x1n)m−1⋅(x1n)′=mxmn−1n⋅1nx1n−1_ (∵上の例題)=mnxmn−1=rxr−1
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |