高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |

1.微分係数と導関数
1.1 微分係数
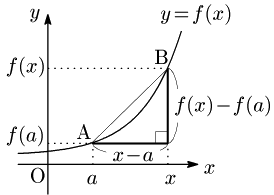
a を固定し,x→a としたとき,平均変化率 f(x)−f(a)x−a⋯① が極限値をもつとき,f(x) は x=a で微分可能であるという.また,①を f′(a) で表す:
f′(a)=limx→af(x)−f(a)x−a
補足
上の x の代わりに a+h とすれば, f(x)−f(a)x–a=f(a+h)−f(a)h と書くことができる.(分母が h だけの方が,約分に気付きやすいことがある.)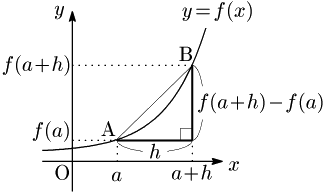
f′(a)=limh→0f(a+h)−f(a)h
例題 f(x)=x3 のとき,f′(1) を求めよ.
その1 f′(1)=limx→1x3−1x−1=limx→1(x−1)(x2+x+1)x−1=limx→1(x2+x+1)=3
その2 f′(1)=limh→0(1+h)3−13h=limh→0h(3+3h+h2)h=limh→0(3+3h+h2)=3
定理 f(x)がx=aで微分可能⇒f(x)はx=aで連続
証明
limx→a{f(x)−f(a)}=limx→af(x)−f(a)x−a⋅(x−a)=f′(a)⋅0=0
■
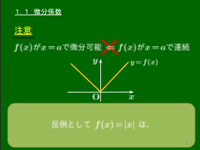
注意
逆 (⇐) は成り立たない.反例として,f(x)=|x| は x=0 で連続だが,x=0 で微分可能ではない.

1.2 導関数
関数 y=f(x) がある区間内の任意の x で微分可能であるとき, limh→0f(x+h)−f(x)h を f(x) の導関数といい, f′(x), y′ ,dydx, ddxf(x) などで表す.また,f(x) の導関数を求めることを「 f(x) を微分する」という.

1.3 導関数の性質
導関数の性質 [1] {kf(x)}′=kf′(x) (kは定数)[2] {f(x)+g(x)}′=f′(x)+g′(x)
証明
[1] {kf(x)}′=limh→0kf(x+h)−kf(x)h=limh→0k⋅f(x+h)−f(x)h=kf′(x)
[2] {f(x)+g(x)}′=limh→0f(x+h)+g(x+h)−{f(x)+g(x)}h=limh→0{f(x+h)−f(x)h+g(x+h)−g(x)h}=f′(x)+g′(x)
■

1.4 積の導関数
積の導関数{f(x)g(x)}′=f′(x)g(x)+f(x)g′(x)
証明
F(x)=f(x)g(x) とおいて,F′(x)=limh→0F(x+h)−F(x)h を計算する. F(x+h)−F(x)=f(x+h)g(x+h)−f(x)g(x)={f(x+h)−f(x)}g(x+h)+f(x){g(x+h)−g(x)} であるから, F(x+h)−F(x)h=f(x+h)−f(x)hg(x+h)+f(x)g(x+h)−g(x)h→ f′(x)g(x)+f(x)g′(x) (h→0)
■
注意
{f(x)g(x)}′=f′(x)g′(x) ではない.
例題 関数 y=(x2+1)(x2−3x+2) を微分せよ.
\begin{align*} y’&=(x^2+1)'(x^2-3x+2)+(x^2-1)(x^2-3x+2)’\\[5pt] &=2x(x^2-3x+2)+(x^2+1)(2x-3)\\[5pt] &=\underline{\boldsymbol {4x^3-9x^2+6x-3}} \end{align*}
公式 n が自然数のとき, (x^n)’=nx^{n-1}
証明
(x^n)’=nx^{n-1}\cdots①を帰納法で示す.
n=1 のとき,①の両辺は共に1となり成立.
n=k のとき,①の成立を仮定すると,n=k+1 のとき,
\begin{align*}
\mbox{①の左辺}&=(x^{k+1})’\\[5pt]
&=(x^k\times x)’\\[5pt]
&=(x^k)’\cdot x+x^k\cdot(x)’\ \leftarrow\mbox{積の導関数}\\[5pt]
&=\underline{kx^{k-1}}\cdot x+x^k\cdot1\ \leftarrow\mbox{帰納法の仮定}\\[5pt]
&=(k+1)x^k\\[5pt]
&=\mbox{①の右辺}
\end{align*}
となるからこのときも成立.
以上により,任意の自然数 n で①は成立.
■

1.5 商の導関数
商の導関数(1) \left\{\frac 1{g(x)}\right\}’=-\frac{g'(x)}{\{g(x)\}^2}
証明
F(x)=\dfrac1{g(x)} とおいて,F'(x) を考える. \begin{align*} F(x+h)-F(x)&=\frac1{g(x+h)}-\frac1{g(x)}\\[5pt] &=-\frac{g(x+h)-g(x)}{g(x+h)g(x)} \end{align*} であるから, \begin{align*} \frac{F(x+h)-F(x)}h&=-\frac{g(x+h)-g(x)}h\cdot\frac1{g(x+h)g(x)}\\[5pt] &\to -g'(x)\cdot\frac1{\{g(x)\}^2}\ \ (h\to0) \end{align*}
■
この結果を用いて次が示される:
商の導関数(2) \left\{\frac{f(x)}{g(x)}\right\}’=\frac{f'(x)g(x)-f(x)g'(x)}{\{g(x)\}^2}
証明
\dfrac{f(x)}{g(x)}=f(x)\cdot\dfrac1{g(x)} として積の導関数の公式を用いると, \begin{align*} \left(\frac fg\right)’&=f’\cdot\frac1g+f\cdot\left(\frac1g\right)’\ \leftarrow\mbox{積の導関数}\\[5pt] &=\frac{f’}g-\frac{fg’}{g^2}\\[5pt] &=\frac{f’g-fg’}{g^2} \end{align*}
■
例
例1 \left(\dfrac1{x^2+3x}\right)’=-\dfrac{(x^2+3x)’}{(x^2+3x)^2}=\underline{-\dfrac{2x+3}{(x^2+3x)^2}}
例2 \left(\dfrac x{x^2+1}\right)’=\dfrac{(x)'(x^2+1)-x(x^2+1)’}{(x^2+1)^2}=\underline{\dfrac{-x^2+1}{(x^2+1)^2}}
公式 n が整数のとき, (x^n)’=nx^{n-1}
証明
n が自然数のときは証明済み.
よって整数 n が n\leqq0 のとき,(x^n)’=nx^{n-1}\cdots ① が成り立つことを示す.
n=0 のとき,①の両辺は共に0だから成立.
n < 0 のとき,n=-m とおくと,m > 0 だから,
\begin{align*}
(x^n)’&=(x^{-m})’\\[5pt]
&=\left(\frac1{x^m}\right)’\\[5pt]
&=-\frac{(x^m)’}{(x^m)^2}\ \leftarrow\mbox{商の導関数}\\[5pt]
&=-\frac{mx^{m-1}}{x^{2m}}\\[5pt]
&=-mx^{-m-1}\\[5pt]
&=nx^{n-1}
\end{align*}
以上により,n\leqq0 のときも①は成立.
■
例
\left(\frac1{x^2}\right)’=\left(x^{-2}\right)’=-2x^{-3}=-\frac2{x^3}
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |