高校数学[総目次]

数学B　第3章　統計的な推測

  スライド ノート 問題
1. 確率変数と確率分布      
2. 確率変数の期待値と分散      
3. 確率変数の変換      
4. 確率変数の和と期待値      
5. 独立な確率変数と期待値・分散      
6. 二項分布      
7. 正規分布      
8. 母集団と標本     [会員]
9. 推定      
10. 仮説検定      

8．母集団と標本

8.1　標本

標本調査と全数調査

　統計的な調査には，調査対象の全数を調べる全数調査と，調査対象の一部を調べて全体を推測する標本調査がある．

　全数調査で有名なのが，5年に1度の国勢調査である．一方，テレビの視聴率といったものは標本調査である．

　調査対象を正確に知るには全数調査がよいと思うかもしれないが必ずしもそうではない．調査対象が日本人全体といった場合には莫大な費用と時間を要するし，あるいは製品の耐用年数の検査の場合には全製品を壊れるまで使い続けなければならず，全数調査がそもそも意味を持たなくなってしまう．また，経済成長率のように現時点で測定不可能な要素を含む場合もある．

標本調査におけるいくつかの用語

　母集団：調査対象全体
　標本　：母集団から選ばれた要素の集合
　抽出　：母集団から標本を抜き出すこと
　母集団の大きさ：母集団の要素の個数
　標本の大きさ　：標本の要素の個数
　無作為抽出：調査対象をランダムに選ぶこと
　無作為標本：無作為抽出によってえらばれた標本

8.2　母集団分布

まずは例　～数学Ⅰデータの分析の復習～

　あるクラスの40人の生徒に対して，1週間のうち何回公園を訪れるかを調査したところ次の表のような結果を得た．

回数$0\ \ \ \ 1\ \ \ \ 2\ \ \ \ 3\ \ \ \ 4$計
度数$6\ \ \ 6\ \ \ 14\ \ 10\ \ \ 4$$40$

　これらのデータから，公園を訪れる回数の平均値 $m$，分散 $s^2$，標準偏差 $s$ は数学Ⅰ データの分析で学んだように次のように計算される：

\[\begin{align*} m&=\frac1{40}(0\cdot6+1\cdot6+2\cdot14+3\cdot10+4\cdot4)\\[5pt] &=\frac{80}{40}=2\\[5pt] s^2&=\frac1{40}\{(0\!-\!2)^2\!\cdot\!6\!+\!(1\!-\!2)^2\!\cdot\!6\!+\!(2\!-\!2)^2\!\cdot\!14\!+\!(3\!-\!2)^2\!\cdot\!10\!+\!(4\!-\!2)^2\!\cdot\!4\}\\[5pt] &=\frac{56}{40}=1.4\\[5pt] s&=\sqrt{1.4} \end{align*} \]
相対度数分布から確率分布へ

　ここで，この40人から無作為に1人を選ぶと，その生徒が公園を訪れる回数は0,1,2,3,4のいずれかであり，そのどれになるかは確率の問題である．公園を訪れる回数を $X$ とすると，確率は相対度数で求められる：

$X$$0\hspace{6mm}1\hspace{6mm}2\hspace{6mm}3\hspace{6mm}4$計
相対度数$\dfrac6{40}\ \ \ \dfrac6{40}\ \ \ \dfrac{14}{40}\ \ \ \dfrac{10}{40}\ \ \ \dfrac4{40}$$1$

　つまり$X$ は「40人から1人を選ぶ」という試行の結果得られる数であり，その背後に確率が1つ対応しているのであるから確率変数であると考えることができる．そして $X$ が従う分布はすぐ上の表から次のようになる．

$X$$0\hspace{6mm}1\hspace{6mm}2\hspace{6mm}3\hspace{6mm}4$計
$P$$\dfrac6{40}\ \ \ \dfrac6{40}\ \ \ \dfrac{14}{40}\ \ \ \dfrac{10}{40}\ \ \ \dfrac4{40}$$1$
$X$ が従う分布
「相対度数」を「$P$」に書き換えただけ

　このとき確率変数 $X$ の期待値 $E(X)$，分散 $V(X)$，標準偏差 $\sigma(X)$ はそれぞれ次のように計算される．

\[\begin{align*} E(X)&=0\cdot\frac6{40}+1\cdot\frac6{40}+2\cdot\frac{14}{40}+3\cdot\frac{10}{40}+4\cdot\frac3{40}\\[5pt] &=\frac{80}{40}=2\\[5pt] V(X)&=(0\!-\!2)^2\!\cdot\!\frac6{40}\!+\!(1\!-\!2)^2\!\cdot\!\frac6{40}\!+\!(2\!-\!2)^2\!\cdot\!\frac{14}{40}\!+\!(3\!-\!2)^2\!\cdot\!\frac{10}{40}\!+\!(4\!-\!2)^2\!\cdot\!\frac4{40}\\[5pt] &=\frac{56}{40}=1.4\\[5pt] \sigma(X)&=\sqrt{V(X)}=\sqrt{1.4} \end{align*} \]

　以上により，

\[\begin{align*} E(X)&=m\\[5pt] V(X)&=s^2\\[5pt] \sigma(X)&=s \end{align*}\]

であることがわかる．

ここから一般論　～母集団分布とは～

　一般に，大きさ $N$ の母集団において，変量 $x$ のとり得る値で異なるものが

\[x_1,\ \ x_2,\ \ \cdots,\ \ x_n\]

の $n$ 個であるとし，それぞれの値をとる度数，すなわちその値をとる要素の個数が順に

\[f_1,\ \ f_2,\ \ \cdots,\ \ f_n\]

であるとする．これは全数調査であるから

\[f_1+f_2+\cdots+f_n=N\]

である．また表にまとめると次のようになる．

変量$x_1\ \ \ x_2\ \ \ \cdots\ \ \ x_n$計
度数$f_1\ \ \ f_2\ \ \ \cdots\ \ \ f_n$$N$

　変量 $x$ の分布は次のように相対度数で求めることができる．

変量$x_1\ \ \ \ x_2\ \ \ \ \cdots\ \ \ \ x_n$計
$P$$\dfrac{f_1}N\ \ \ \dfrac{f_2}N\ \ \ \cdots\ \ \ \dfrac{f_n}N$$1$

　これをこの母集団における変量 $x$ の母集団分布という．またその平均値，分散，標準偏差をそれぞれ母平均，母分散，母標準偏差という．

母集団から抽出された大きさ1の無作為標本の確率分布は，母集団分布と一致する

　いまこの母集団から無作為に1つの要素を抽出し，その要素の変量の値を $X$ とすると，$X$ は「大きさ1の無作為抽出」という試行の結果から得られる数であるから確率変数であると考えることができる．$X$ が従う分布は相対度数から次のようになる．

$X$$x_1\ \ \ \ x_2\ \ \ \ \cdots\ \ \ \ x_n$計
$P$$\dfrac{f_1}N\ \ \ \dfrac{f_2}N\ \ \ \cdots\ \ \ \dfrac{f_n}N$$1$
$X$ が従う分布

　見ての通り，すぐ上にあげた2つの分布は完全に同一のものとなっている．換言すれば

「母集団分布」と「大きさ1の無作為標本の確率分布」は一致している

ということである．従って確率変数 $X$ の期待値 $E(X)$，分散 $V(X)$，標準偏差 $\sigma(X)$ と，母平均 $m$，母分散 $\sigma^2$，母標準偏差 $\sigma$ との関係は次のようになる．

\[\begin{align*} E(X)&=m\\[5pt] V(X)&=\sigma^2\\[5pt] \sigma(X)&=\sigma \end{align*}\]

例題　10枚のカードがあり，調べてみると0，1，2が書かれたカードがそれぞれ5枚，2枚，3枚の計10枚であった．この10枚を母集団，カードの数字を変量とするとき，母平均，母分散，母標準偏差を求めよ．

8.3　復元抽出と非復元抽出

復元抽出と非復元抽出

　母集団から標本を抽出するとき，毎回元に戻して抽出を繰り返す方法を復元抽出といい，元に戻さないで抽出していく方法を非復元抽出という．

例　1から10の各数字が書かれた10枚のカードから，大きさ3の標本を抽出するとき，

復元抽出　：$10^3=1000$ 通りの標本ができる．
非復元抽出：選ぶ順番を考慮すると$_{10}{\rm P}_3=720$ 通りの標本ができる

補足

　非復元抽出は，厳密には独立試行とならないが，抽出回数に比べて母集団の大きさが十分大きいとき，前の抽出結果が後の抽出にほとんど影響しないと考えて近似的に復元抽出と同様に独立試行であると考える場合がある．

8.4　標本平均

$n$回の復元抽出により得られた$n$個の確率変数は，すべて同じ分布に従う

　母集団(という集合)から大きさ $n$ の無作為標本を抽出する，すなわち無作為に $n$ 個の要素を取り出して集合を作る．この $n$ 個について，変量 $x$ の値を $X_1,X_2,\cdots,X_n$ とすると，これらは標本からの抽出という試行の結果によって定まる確率変数である．

　例えば，1から6の各数字が書かれたカードが1枚ずつ，計6枚あるとしてこれを母集団とする．ここからカードを無作為に1枚ずつ取り出しては戻すという操作を10回行い，$i$ 回目に取り出されたカードの数字を $X_i$ $(i=1,2,\cdots,10)$ とすると，これらは確率変数となり，各 $X_i$ は すべて同じ分布に従う：

$X_i$$1\ \ \ \ 2\ \ \ \ 3\ \ \ \ 4\ \ \ \ 5\ \ \ \ 6$計
$P$$\dfrac16\ \ \dfrac16\ \ \dfrac16\ \ \dfrac16\ \ \dfrac16\ \ \dfrac16$$1$
$X_i$ が従う確率分布
標本平均と標本標準偏差

　次に，標本平均と標本標準偏差について説明する．標本平均 $\overline{X}$ と標本標準偏差 $s$ を次のように定義する．

標本平均と標本標準偏差 \[\begin{align*} &\overline{X}=\frac{X_1+X_2+\cdots+X_n}n\\[5pt] &s=\sqrt{\frac1n\sum_{k=1}^n(X_k-\overline{X})^2} \end{align*}\]

　これらは定義式からわかるように，観測された $n$ 個のデータについての平均値と標準偏差である．また標本分散は標本標準偏差の2乗で $\displaystyle\frac1n\sum_{k=1}^n(X_k-\overline{X})^2$ となっている．標本平均 $\overline{X}$ については次に示すように期待値 $E(\overline{X})$ が母平均に一致するが，標本分散についてはその期待値 $\displaystyle E\left(\frac1n\sum_{k=1}^n(X_k-\overline{X})^2\right)$ が母分散と一致していない．詳しくはこのページの最も下にあるコラム～不偏分散を参照．

■標本平均の期待値と分散

これ以降の主役は標本平均

　標本平均と標本標準偏差という2つの統計量を確認したが，今後我々の興味・関心は専ら標本平均である．

　標本平均は例えば100個のデータを抽出したとしても，どのデータが抽出されたかによって値は確率的に変わるものであって，従って標本平均も1つの確率変数である．そこで標本平均という確率変数の期待値と分散がどうなっているのか見ていこう．

　ある母集団から大きさを $n$ の無作為標本を復元抽出し，変量 $x$ の値を $X_1,X_2,\cdots,X_n$ とする．母平均を $m$，母標準偏差を $\sigma$ とすれば，各 $X_i$ $(i=1,2,\cdots,n)$ はすべて同じ分布(母集団分布)に従うから，すべての $\boldsymbol i$ で，

\[\begin{align*} &E(X_i)=m\\[5pt] &\sigma(X_i)=\sigma \end{align*}\]

である．従って，標本平均 $\overline{X}$ の期待値は，

\[\begin{align*} E(\overline{X})&=E\left(\frac{X_1+X_2+\cdots+X_n}n\right)\\[5pt] &=\frac{E(X_1)+E(X_2)+\cdots+E(X_n)}n\\[5pt] &=\frac{nm}n\\[5pt] &=m \end{align*}\]

　また，復元抽出では$X_1,X_2,\cdots,X_n$ は互いに独立であるから，

\[\begin{align*} V(\overline{X})&=V\left(\frac{X_1+X_2+\cdots+X_n}n\right)\\[5pt] &=\frac{V(X_1)+V(X_2)+\cdots+V(X_n)}{n^2}\\[5pt] &=\frac{n\sigma^2}{n^2}\\[5pt] &=\frac{\sigma^2}n\\[5pt] \therefore \sigma(\overline{X})&=\sqrt{V(\overline{X})}=\frac\sigma{\sqrt n} \end{align*}\]

　ここでは復元抽出を仮定したが，母集団の大きさが標本の大きさ $n$ に比べて十分大きいときは，非復元抽出であっても近似的に復元抽出として考えることもある．

まとめ　母平均 $m$，母標準偏差 $\sigma$ の母集団から大きさ $n$ の無作為標本を抽出するとき，標本平均 $\overline{X}$ の期待値と標準偏差は \[\begin{align*} E(\overline{X})&=m\\[5pt] \sigma(\overline{X})&=\frac\sigma{\sqrt n} \end{align*}\]

補足

　上の式から，標本の大きさ $n$ を大きくすると，標本平均 $\overline{X}$ の散らばり具合である標準偏差は0に近付いていくことがわかる．

例題　ある県の小学生全員を対象に鉛筆を何本持っているかを調査したところ，平均値(母平均)は40本，標準偏差(母標準偏差)は8本であることがわかった．この母集団から無作為に100人を選んだとき，この100人が持っている鉛筆の本数の平均 $\overline{X}$ の期待値 $E(\overline{X})$ と標準偏差 $\sigma(\overline{X})$ を求めよ．

8.5　標本平均の分布と正規分布

確率変数$X_1+X_2+\cdots+X_n$は正規分布にどんどん近付く

　母平均 $m$，母分散 $\sigma^2$ の母集団から，大きさ $n$ の無作為標本を抽出し，それらの変量の値を $X_1,X_2,\cdots, X_n$ とすると，これらはみな同じ分布(母集団分布)に従う確率変数である．いまこれら $n$ 個の確率変数の和をとり

\[X=X_1+X_2+\cdots+X_n\]

とすると $X$ もまた確率変数である．

　ところでこのように確率変数の和をとることは，統計学において大変重要な意味を有している．どういうことか？

　実は $n$ の値を大きくしていくと，確率変数 $X$ はどんどん正規分布に近付いていくのである．しかも母集団分布がいかなる分布であっても！である．この事実はある母集団から抽出した大きさ $n$ の無作為標本の平均値

\[\overline{X}=\dfrac{X_1+X_2+\cdots+X_n}n\]

でも成り立つ．そのことを例で確認してみよう．

標本平均の分布が正規分布に近付いていく様子

　さいころを何回か投げることを考える．確率変数 $X_k$ を $k$ 回目出た目とする．$X_k$ のとりうる値は 1から6の6つである．

　さいころを1回だけ投げる場合，どの目が出る確率も $\dfrac16(=0.166\cdots)$ となっており，確率分布は次のグラフのようになっている．

$X_1$ が従う分布

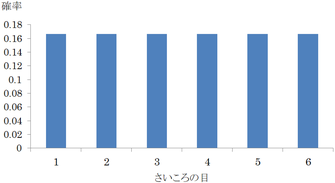
　この段階では正規分布の影もない．

　次に，さいころを2回投げたときの標本平均 $\dfrac{X_1+X_2}2$，すなわち2回の出た目の平均値を考える．さいころを2回投げたとき，全部の目の出方は $6\times6=36$ 通りあって，出た目の合計は $2,3,4,\cdots 12$ の11通りある．平均値は2で割って $1.0,1.5,2.0,\cdots6.0$ である．$\dfrac{X_1+X_2}2$ の確率分布を

\[P(X_1+X_2=k)=\left\{ \begin{array}{ll} \dfrac{k-1}{36}&(2\leqq k\leqq7)\\[5pt] \dfrac{13-k}{36}&(8\leqq k\leqq 12) \end{array}\right. \]

によって計算すると次のようになる．

$\dfrac{X_1+X_2}2$ が従う分布

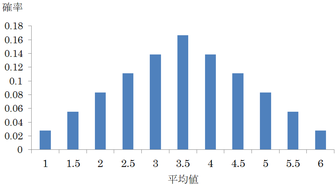
　2回の平均値で既に正規分布の特徴である山型が出現している．

　そして5回投げた平均値 $\dfrac{X_1+X_2+X_3+X_4+X_5}5$ のグラフが次である．

$\dfrac{X_1+X_2+X_3+X_4+X_5}5$ が従う分布

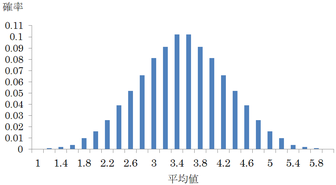
　さいころをたった5回投げただけであるにもかかわらず，一見しただけでは正規分布のグラフと見分けがつかない．

　一般に，標本平均 $\overline{X}=\dfrac{X_1+X_2+\cdots+X_n}n$ について，次の事実が知られている．

定理 　母平均 $m$，母分散 $\sigma^2$ の母集団から，大きさ $n$ の無作為標本を抽出する．$n$ が十分に大きいとき，標本平均 $\overline{X}$ は近似的に正規分布 $N\left(m,\dfrac{\sigma^2}n\right)$ に従うとみなすことができる．

補足

　$\overline{X}=\dfrac{X_1+X_2+\cdots+X_n}n$ ではなく，$X=X_1+X_2+\cdots+X_n$ については，近似的に正規分布 $N(nm,n\sigma^2)$ に従う．

中心極限定理

　上に挙げた定理は中心極限定理(central limit theorem)と呼ばれ，統計学において最も重要な定理の一つである．この定理は母集団分布が何であっても $n$ が十分に大きいときには $X$ 及び $\overline{X}$ が概ね正規分布に従うというもので，偶発的に得られる値の背後にこのような法則があるとは驚きというほかない．
　尚，母集団分布が正規分布とわかっているときには，$n$ の大きさによらず常に正規分布 $N\left(m,\dfrac{\sigma^2}n\right)$ に近似的にではなく正確に従うことが知られている．

例題　ある県の小学生全員を対象に消しゴムを何個持っているかを調査したところ，平均値(母平均)は10個，標準偏差(母標準偏差)は4個であることがわかった．この母集団から無作為に100人を選んだとき，この100人が持っている消しゴムの個数の平均 $\overline{X}$ が12個以上である確率を求めよ．

母比率と標本比率

母比率・標本比率とは

　母集団において，ある特性をもつ割合を母比率という．母集団から抽出された標本の中で，その特性をもつ割合を標本比率という．

　ある特性Aをもつ母比率が $p$ である母集団から大きさ $n$ の無作為標本を抽出したとき，特性Aをもつ個数が $S$ であるとすれば，標本比率というのは $\dfrac Sn$ のことである．いまこれを $R$ とおく：

\[R=\frac Sn\]

標本比率は二項分布に従う確率変数で表される

　いま母集団の大きさが $n$ と比べて十分大きいとするならば，各回の抽出が独立試行とみなすことができたから(復元抽出と非復元抽出 )，特性Aをもつ個数が $S$ であったというのは，$n$ 回の無作為抽出という反復試行で特性Aをもつ個体が抽出された回数が $S$ であったと言い換えることができる．これは例えばさいころを $n$ 回投げたとき1の目が出る回数を考えるときと状況が似ている．従って $S$ は二項分布 $B(n,p)$ に従う確率変数で，平均は $np$，分散は $np(1-p)$ であるから

\[\begin{align*} &E(R)=E\left(\frac Sn\right)=\frac{E(S)}n=\frac{np}n=p\\[5pt] &V(R)=V\left(\frac Sn\right)=\frac{V(S)}{n^2}=\frac{np(1-p)}{n^2}=\frac{p(1-p)}n \end{align*}\]

となる．

$n$を大きくして二項分布から正規分布に近似

　二項分布に従う確率変数は $n$ が十分大きいとき，近似的に正規分布に従うのであった(二項分布の正規分布による近似 )．よって $n$ が大きいとき，標本比率 $R$ は近似的に正規分布 $N\left(p,\dfrac{p(1-p)}n\right)$ に従う．

母比率と正規分布　母比率が $p$ である母集団から大きさ $n$ の無作為標本を抽出すると，標本比率 $R$ は $n$ が大きいとき近似的に正規分布 $N\left(p,\dfrac{p(1-p)}n\right)$ に従う．

いくつかの例

例1 [テレビの視聴率]

　あるテレビ番組Aを見た世帯の割合が30%(母比率が0.3)である地域があるとする．いまこの地域から大きさ100の無作為標本を抽出し，それらの変量 $x$ を

番組Aを観たとき　　　$X_i=1$
番組Aを観てないとき　$X_i=0$

とする．$X_1,X_2,\cdots,X_{100}$ は互いに独立で，すべて同一の確率分布 $P(X_i=1)=0.3,P(X_i=0)=0.7$ に従うと考えてよい．ここで

\[S=X_1+X_2+\cdots+X_{100}\]

とおけば，$S$ は抽出された $100$ 世帯の中に番組Aを観た世帯数を表す確率変数で，二項分布 $B(100,0.3)$ に従う．

　標本比率 $\dfrac S{100}$ の平均と分散は次のようになる．

\[\begin{align*} E\left(\frac S{100}\right)&=\frac{E(S)}{100}=\frac{100\times0.3}{100}=0.3\\[5pt] V\left(\frac S{100}\right)&\!=\!\frac{V(S)}{100^2}\!=\!\frac{100\!\cdot\!0.3(1\!-\!0.3)}{100^2}\!=\!\frac{0.3\!\times\!0.7}{100}\!=\!0.0021\\[5pt] \sigma\left(\frac S{100}\right)&=\sqrt{V\left(\frac S{100}\right)}=\sqrt{0.0021}\fallingdotseq 0.046 \end{align*}\]

　よって，観測された標本比率 $\dfrac S{100}$ はほぼ $30\%\pm4.6\%$ 程度になると期待される．たった100世帯の情報から全体の情報をある程度の精度で見積もることができるのである．そして次節で学ぶ大数の法則によれば，標本の大きさ $n$ を大きくしていくとどんどん母平均 $0.3$ に近付いていく．

　このように標本平均は全体の一部しか見ていないにもかかわらず，母平均をかなりの精度で推定できるということが，統計学から得られた知見である．

例2 [りんご農園で基準に満たないりんごの割合]

　あるりんご農園で行う選定作業において，基準に満たない母比率が $0.1$ であるとわかっているとき，100個収穫した際に出荷できない個数は二項分布 $B(100,\ 0.1)$ に従う．このとき平均と分散は

\[\begin{align*} &100\times0.1=10,\\[5pt] &100\times0.1\times(1-0.1)=9 \end{align*}\]

となるから， サンプルのために収穫した100個のうち，基準に満たないものの個数は近似的に正規分布 $N(10,9)$ に従う．

　また，標本比率の平均 $E$ と分散 $V$ は次のようになる．

\[\begin{align*} E&=0.1\\[5pt] V&=\frac{0.1(1-0.1)}{100}=0.0009 \end{align*}\]

　従って，サンプルとして収穫したものに含まれる基準に満たない個数の割合(標本比率)は正規分布 $N(0.1,\ 0.0009)$ に従う．

補足

二項分布に従う確率変数は，$n$個の確率変数の和として表すことができるから正規分布に近似できる

　ここで二項分布 $B(n,p)$ に従う確率変数 $S$ が，$n$ が十分大きいとき近似的に正規分布 $N(np,np(1-p))$ に従うことを詳しく見ておこう．

　$X_i\ (i=1,2,\cdots, n)$ を，$i$ 番目の標本が特性Aをもてば $X_i=1$，もたなければ $X_i=0$ とすると，すべての $i$ について $X_i$ は二項分布 $B(1,p)$ に従う確率変数であり，

\[E(X_i)=p,\ \ V(X_i)=p(1-p)\]

である．ここで

\[S=X_1+X_2+\cdots +X_n\]

とすれば，母集団の大きさが十分大きいとき $X_1,X_2,\cdots,X_n$ は互いに独立と考えてよいから(復元抽出と非復元抽出 )

\[\begin{align*} E(S)&=E(X_1)+E(X_2)+\cdots+E(X_n)\\[5pt] &=np,\\[5pt] V(S)&=V(X_1)+V(X_2)+\cdots+V(X_n)\\[5pt] &=np(1-p) \end{align*} \]

となる．$X_i$ はすべて同じ分布に従う互いに独立な確率変数であるから，それらの和である $S$ は中心極限定理により近似的に正規分布 $N(np,np(1-p))$ に従うのである．

　ところで $S$ のように $n$ 回の反復試行(抽出)で特性Aをもつものが選ばれる回数を表す確率変数は二項分布 $B(n,p)$ に従うのであった．

　要するに二項分布に従う確率変数というのは，互いに独立でかつ同一の分布に従う確率変数の和として表わすことができるため，$n$ が大きいときは中心極限定理によって近似的に正規分布に従うのである．

8.6　大数の法則

大数の法則とは

　前節で述べた定理(中心極限定理)は，標本平均 $\overline{X}$ が近似的に $N\left(m,\dfrac{\sigma^2}n\right)$ に従うというものであったが， $n$ を大きくしていくと，$\overline{X}$ は $m$ の付近に集中していく．つまり，$\overline{X}$ が $m$ に近い値をとる確率を，$n$ を大きくすることでいくらでも1に近付けることができるということである．これを大数の法則(たいすうのほうそく，law of large numbers)という．

大数の法則　母平均 $m$ の母集団から大きさ $n$ の無作為標本を抽出するとき，標本平均 $\overline{X}$ は $n$ が大きくなるにつれて母平均 $m$ に近付く．

大数の法則が主張する具体的な内容

　例えば，硬貨を $n$ 回投げて，表が出る割合(確率)を考える．理論上表の出る割合(確率)は $\dfrac12$ だが，実際に $n$ 回投げたうちのちょうど半分が表という訳ではない．

　確率変数 $X_k$ を

$k$ 回目に表が出れば， $X_k=1$
$k$ 回目に裏が出れば， $X_k=0$

とし，

\[X=X_1+X_2+\cdots+X_n\]

とすると，$X$ は観測された表の出る回数を表し，二項分布 $B\left( n,\dfrac12\right)$ に従うから， $X=x$ となる確率は

\[_n{\rm C}_x\left(\frac12\right)^n\]

である．

　今，10回$(n=10)$投げるとすれば，表の出る割合は $0.0, 0.1, 0.2, \cdots , 1.0$ の11通りあり，それらの確率は $_{10}{\rm C}_x\left(\dfrac12\right)^{10}$ で計算して $N=2^{10}=1024$ とおけば順に

\[\frac1N,\frac{10}N,\frac{45}N,\frac{120}N,\frac{210}N, \frac{252}N,\frac{210}N,\frac{120}N,\frac{45}N,\frac{10}N,\frac{1}N\]

となる．例えば

\[P\left(0.4\leqq \frac x{10}\leqq 0.6\right)=\frac{210+252+210}{1024}\fallingdotseq0.66\]

であり，真の確率 $\dfrac12$ 周辺の発生割合が高いが，$1-0.66=0.34$ より $34\%$ 程度の確率で $\dfrac12$ から離れた割合となることもわかる．

　ところがこの試行を50回，100回 と増やしていくと，表の出る割合が $0.4$ から $0.6$ となる確率は

\[\begin{align*} &P\left(0.4\leqq\frac x{50}\leqq 0.6\right)\fallingdotseq 0.88\\[5pt] &P\left(0.4\leqq\frac x{100}\leqq 0.6\right)\fallingdotseq 0.97 \end{align*}\]

となって，確率 $\dfrac12$ 付近に集中していく．これが大数の法則で主張している内容である．

コラム～不偏分散とは

　標本平均と標本標準偏差 のところで触れた標本標準偏差の期待値が母標準偏差と一致していないという点について説明したいと思います．ただこの内容は大学で学ぶ内容ですから，大学受験や定期試験では役に立ちません．

　標本標準偏差 $s=\displaystyle\sqrt{\dfrac1n\sum_{k=1}^n(X_k-\overline{X})^2}$ から標本分散 $s^2$ は， $s^2=\displaystyle\frac1n\sum_{k=1}^n(X_k-\overline{X})^2$ となりますが，この式では母分散を正確に評価できていません．どういう意味でしょうか？

　もともと母平均や母分散といったものは事前にわかっていないことが多く、そのため標本平均や標本分散でそれらの値を代用するのですが，その際標本平均 $\overline{X}$ の方は上で見たように，その期待値 $E(\overline{X})$ が母平均 $m$ に一致するのに対して，標本分散 $s^2$ の期待値 $E(s^2)$ は母分散 $\sigma^2$ に一致していないのです．換言すれば，$s^2=\displaystyle\frac1n\sum_{k=1}^n(X_k-\overline{X})^2$ では母分散を正確に評価できていないのです．ではどのように計算すれば正確な評価が得られるのでしょうか？それは

\[{s’}^{\,2}=\frac1{\boldsymbol{ n-1}}\sum_{k=1}^n(X_k-\overline{X})^2\]

というように，$n$ ではなく $n-1$ で割ればよいのです．この ${s’}^{\,2}$ を母分散 $\sigma^2$ の不偏推定量，または不偏分散といいます．これは期待値が母分散に一致しているという意味で正確な評価といえます．計算が長くなりますがこのことを実際に確かめてみましょう．

　$Y_i=X_i-m$ とおくと，

\[\begin{align*} \sum_{i=1}^n(X_i-\overline{X})^2&=\sum_{i=1}^n\{(X_i-m)-(\overline{X}-m)\}^2\\[5pt] &=\sum_{i=1}^n(Y_i-\overline{Y})^2\\[5pt] &=\sum_{i=1}^n({Y_i}^2-2Y_i\overline{Y}+\overline{Y}^2)\\[5pt] &=\sum_{i=1}^n{Y_i}^2-2\overline{Y}\sum_{i=1}^n Y_i+\sum_{i=1}^n\overline{Y}^2\\[5pt] &=\sum_{i=1}^n{Y_i}^2-2n\overline{Y}^2+n\overline{Y}^2\\[5pt] &=\sum_{i=1}^n{Y_i}^2-n\overline{Y}^2 \end{align*}\]

となりますから，期待値をとると

\[\begin{align*} E\left(\sum_{i=1}^n(X_i-\overline{X})^2\right)&=E\left(\sum_{i=1}^n{Y_i}^2-n\overline{Y}^2\right)\\[5pt] &=\sum_{i=1}^nE({Y_i}^2)-nE\Bigl(\overline{Y}^2\Bigr)\ \cdots\mbox{①} \end{align*}\]

となります．ここで，

\[\begin{align*} E(Y_i)&=E(X_i-m)\\[5pt] &=E(X_i)-m\\[5pt] &=m-m\\[5pt] &=0\\[5pt] E(\overline{Y})&=E\left(\frac1n\sum_{i=1}^n(X_i-m)\right)\\[5pt] &=\frac1n\sum_{i=1}^nE(X_i-m)\\[5pt] &=\frac1n\sum_{i=1}^n(m-m)\\[5pt] &=0 \end{align*}\]

となりますから，

\[\begin{align*} E({Y_i}^2)&=E({Y_i}^2)-\{E(Y_i)\}^2\ \ \ (\because E(Y_i)=0)\\[5pt] &=V(Y_i)\\[5pt] &=V(X_i-m)\\[5pt] &=V(X_i)=\sigma^2\\[5pt] E(\overline{Y}^2)&=E(\overline{Y}^2)-\{E(\overline{Y})\}^2\ \ \ (\because E(\overline{Y})=0)\\[5pt] &=V(\overline{Y})\\[5pt] &=\frac{n\sigma^2}{n^2}=\frac{\sigma^2}n \end{align*}\]

　従って①まで戻って，

\[\begin{align*} E\left(\sum_{i=1}^n(X_i-\overline{X})^2\right)&=\sum_{i=1}^nE({Y_i}^2)-nE\Bigl(\overline{Y}^2\Bigr)\\[5pt] &=n\sigma^2-n\cdot\frac{\sigma^2}n\\[5pt] &=(n-1)\sigma^2 \end{align*}\]

　${s’}^{\,2}$ の期待値は，この式を $n-1$ で割れば得られますから，

\[E({s’}^{\,2})=\frac1{n-1}E\left(\sum_{i=1}^n(X_i-\overline{X})^2\right)=\frac{(n-1)\sigma^2}{n-1}=\sigma^2\]

　故に期待値が母分散に一致することが確認できました．

■

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第3章　統計的な推測

  スライド ノート 問題
1. 確率変数と確率分布      
2. 確率変数の期待値と分散      
3. 確率変数の変換      
4. 確率変数の和と期待値      
5. 独立な確率変数と期待値・分散      
6. 二項分布      
7. 正規分布      
8. 母集団と標本     [会員]
9. 推定      
10. 仮説検定