7．正規分布(ノート)｜スライドで学ぶ高校数学

高校数学[総目次]

数学B　第3章　統計的な推測

	スライド	ノート	問題
1. 確率変数と確率分布
2. 確率変数の期待値と分散
3. 確率変数の変換
4. 確率変数の和と期待値
5. 独立な確率変数と期待値・分散
6. 二項分布
7. 正規分布
8. 母集団と標本			[会員]
9. 推定
10. 仮説検定

7．正規分布

7.1　連続型確率変数

連続型確率変数とは

　例えば，日本人の身長のように連続的な値をとるようなものを考え，それを $X$ (cm) とする．そして例えば $160\leqq X\leqq170$ の人の割合(確率)が

\[\int_{160}^{170}f(x)dx\]

で与えられるような関数 $f(x)$ が存在するとき，$X$ を連続型確率変数という．これに対してさいころの目のように，とびとびの値しかとらないような確率変数を離散型確率変数という．

　横軸に身長をとって $f(x)$ のグラフを描くと，そのグラフは曲線となるであろう．この曲線を確率変数 $X$ の分布曲線といい，$f(x)$ を確率密度関数という．

　この確率密度関数 $f(x)$ とは要するに，確率変数が $X=x$ のときの確率を与えるような役割を果たすのであるが，この考え方には注意も必要で，連続型確率変数の場合「$X=x$ のときの確率」などというものはもはや意味をなさない。こういった離散型確率変数との違いにも注意しながら次節以降を見ていこう．

確率密度関数が持つ特徴

　一般に，連続型確率変数 $X$ の確率密度関数 $f(x)$ は，$f(x)\geqq0$ でなければならない．これは確率がどんな場合でも決して負にならないという要請である．また，$X$ のとり得るすべての値の範囲が $\alpha\leqq X\leqq \beta$ のとき，全事象の確率は1であるという要請から

\[\int_\alpha^\beta f(x)dx=1\]

でなければならない．

　そして，$a\leqq X\leqq b$ となる確率は

\[P(a\leqq X\leqq b)=\int_a^b f(x)dx\]

で表される．この定義からわかるように，1点の確率，例えば $X=a$ となる確率は

\[P(X=a)=\int_a^a f(x)dx=0\]

である．これは離散型の確率との著しい違いである．

確率密度関数の性質 　連続型確率変数 $X$ の確率密度関数を $f(x)$ とする．
　　[1] 常に $f(x)\geqq0$
　　[2] $X$ のとり得る値の範囲が $\alpha\leqq X\leqq \beta$ のとき，$\displaystyle\int_\alpha^\beta f(x)dx=1$
　　[3] $P(a\leqq x\leqq b)=\displaystyle\int_a^b f(x)dx$

例題　連続型確率変数 $X$ のとり得る値の範囲が $0\leqq x\leqq2$ で，確率密度関数が $f(x)=kx(x-2)$ (ただし $k$ は定数)で表されているとする．
(1)　$k$ の値を求めよ．
(2)　確率$P(0\leqq X\leqq 1)$ を求めよ．

答

(1)

\[\int_0^2f(x)dx=k\int_0^2x(x-2)dx=-\frac k6(2-0)^3=-\frac43k\]

　よって，$-\dfrac43k=1$ より，$k=-\dfrac34$．

(2)

\[\begin{align*} P(0\leqq X\leqq 1)&=\int_0^1f(x)dx\\[5pt] &=-\frac34\int_0^1x(x-2)\\[5pt] &=-\frac34\int_0^1(x^2-2x)dx\\[5pt] &=-\frac34\left[\frac{x^3}3-x^2\right]_0^1\\[5pt] &=-\frac34\left\{\frac{1^3-0^3}3-(1^2-0^2)\right\}\\[5pt] &=\frac12 \end{align*}\]

連続型確率変数の期待値・分散

　次に連続型確率変数の期待値と分散はどのように計算されるのか見ていくのであるが，その前に離散型確率変数 $X$ の期待値がどのようにして求められたかを復習しよう．

　例えばさいころ1回投げという試行において，確率変数 $X$ を出た目の数とすれば，$X$ の従う分布は次のようになる：

$X$	1	2	3	4	5	6	計
$P$	$\dfrac16$	$\dfrac16$	$\dfrac16$	$\dfrac16$	$\dfrac16$	$\dfrac16$	1

　そしてヒストグラムは次のようになる：

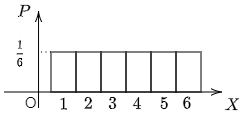
　このとき $X$ の期待値は次のように計算された．

\[E(X)=1\!\cdot\!\frac16\!+\!2\!\cdot\!\frac16\!+\!3\!\cdot\!\frac16\!+\!4\!\cdot\!\frac16\!+\!5\!\cdot\!\frac16\!+\!6\!\cdot\!\frac16\]

　この計算とヒストグラムの対応を見ると，期待値は $X$ の値と，対応する長方形の面積 $\dfrac16$ を掛けて足し合わせたものとなっている．この考え方を連続型確率変数にも拡張する．

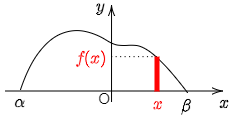
　確率変数 $X$ が，ある値 $x$ を含む微小区間内の値をとるとき，その確率は，高さが $f(x)$で，底辺が微小量 $\Delta x$ の長方形の面積で近似できる．この $x$ の値を連続的に変化させながら $x$，$f(x)$，そして $x$ の微小変化量 $\Delta x$ の3者の積を計算し，次々と足していく．この計算は積分に他ならない．(数学Ⅲ 8.定積分と和の極限 参照)

　連続型確率変数の期待値と分散，標準偏差は次のように定義される：

連続型確率変数の期待値と分散　連続型確率変数 $X$ のとり得る値の範囲が $\alpha\leqq X\leqq\beta$ で，確率密度関数が $f(x)$ のとき， \[E(X)=\int_\alpha^\beta xf(x)dx\] 　また，$m=E(X)$ とすると， \[\begin{align*} V(X)&=\int_\alpha^\beta (x-m)^2f(x)dx\\[5pt] \sigma(X)&=\sqrt{V(X)} \end{align*}\]

例題　連続型確率変数 $X$ の確率密度関数が $f(x)=-\dfrac34x(x-2)$ のとき，期待値，分散，標準偏差を求めよ．

答

\[\begin{align*} E(X)&=\int_0^2 x\left\{-\frac34x(x-2)\right\}dx\\[5pt] &=-\frac34\int_0^2(x^3-2x^2)dx\\[5pt] &=-\frac34\left[\frac{x^4}4-\frac23x^3\right]_0^2\\[5pt] &=-\frac34\left(\frac{16}4-\frac{16}3\right)\\[5pt] &=1\\[5pt] V(X)&=-\frac34\int_0^2(x-1)^2\cdot x(x-2)dx\\[5pt] &=-\frac34\int_0^2(x^4-4x^3+5x^2-2x)dx\\[5pt] &=-\frac34\left[\frac{x^5}5-x^4+\frac53x^3-x^2\right]_0^2\\[5pt] &=\frac15\\[5pt] \sigma(X)&=\sqrt{\frac15}=\frac1{\sqrt5} \end{align*}\]

7.2　正規分布

正規分布とは

　正規分布と呼ばれる連続型の確率分布がある．自然科学や社会科学の多くの分野で利用されており，統計の理論上でも基礎となる分布である．この分布について理論的な側面を詳細に知るには高校の学習範囲を超える数学的な知識が必要となる．

　$m$ を実数，$\sigma$ を正の実数とするとき，

\[f(x)=\frac1{\sqrt{2\pi}\sigma}e^{-\frac{(x-m)^2}{2\sigma^2}}\]

を確率密度関数にもつ連続型確率変数 $X$ は，正規分布 $N(m,\sigma^2)$ に従うという．カッコの前の $N$ は英語で正規分布を意味する normal distribution の $N$ である．

正規分布の確率密度関数についてのいくつかの補足

　いくつかの補足をする．

　まず第一に，$X$ のとり得る値の範囲は実数全体であり，$f(x)$ の最初に出てくる $\dfrac1{\sqrt{2\pi}\sigma}$ の部分は

\[\int_{-\infty}^\infty f(x)dx=1\]

とするための定数である．

　次に，$f(x)$ にある $e$ の指数部分が見にくくなっているが，$X=\dfrac{(x-m)^2}{2\sigma^2}$ とすれば，$e^{-X}$ となっている．

　3つ目に，$E(X)=m,\ V(X)=\sigma^2$ である．これを定義通り計算して確かめるには高校数学では足りない．とにかく，$N(m,\sigma^2)$ というのは，期待値(平均) $m$，分散 $\sigma^2$ の正規分布を意味するのである．

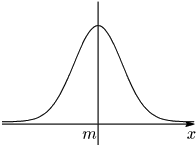
　$f(x)$ のグラフは次のような特徴がある．

7.3　標準正規分布

確率変数の標準化

　確率変数 $X$ が正規分布 $N(m,\sigma^2)$ に従うとする．このとき，確率変数を $Z$ を

\[Z=\frac{X-m}\sigma\]

とすると，確率変数 $Z$ は正規分布 $N(0,1)$ に従うことが知られている．期待値(平均)0，標準偏差1の正規分布 $N(0,1)$ を標準正規分布という．

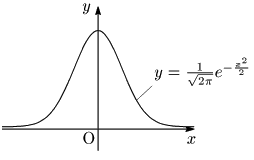
重要 　確率変数 $X$ が正規分布 $N(m,\sigma^2)$ に従うとする．$Z=\dfrac{X-m}\sigma$ とおくと，$Z$ は標準正規分布 $N(0,1)$ に従う．

　今後，あらゆる正規分布の確率計算も、この標準正規分布に帰着させて行う．

　標準正規分布 $N(0,1)$ に従う確率変数 $Z$ について，$P(0\leqq Z\leqq u)$ の値を $p(u)$ とすると，この値の近似値の表がどの教科書の巻末にも与えられている．こういった表の参照は、これまでにも常用対数表で経験しているところであろう．

7.4　二項分布の正規分布による近似

二項分布は正規分布に近付いていく

　二項分布 $B(n,p)$ は，期待値(平均) $np$，分散 $np(1-p)$ となるのであった．（二項分布の期待値と分散）

　例として，さいころを $n$ 回投げたとき1の目が出る回数を $X$ とすると， $X$ は二項分布 $B(n,\frac16)$ に従う確率変数である．ここで $n$ として10，30，50の分布曲線を描くと次のようになる．

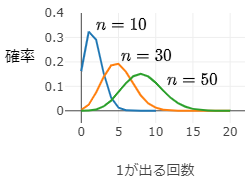
　この図をみると，$n$ の値が増加するにつれてきれいな釣り鐘状のグラフとなっていき，$n=50$ では一見すると正規分布と区別がつかないくらい良く似通っている．

　実は，次節で学ぶ中心極限定理により二項分布は $n$ が大きくなれば，いかなる $p$ であっても正規分布 $N(np,np(1-p))$ に近付くことが知られている．

　従って $n$ の値がある程度大きい二項分布の確率計算は，まず正規分布に帰着させ，更にはそこから標準化を行って標準正規分布にまでもっていって行うこととなる．

高校数学[総目次]

数学B　第3章　統計的な推測

	スライド	ノート	問題
1. 確率変数と確率分布
2. 確率変数の期待値と分散
3. 確率変数の変換
4. 確率変数の和と期待値
5. 独立な確率変数と期待値・分散
6. 二項分布
7. 正規分布
8. 母集団と標本			[会員]
9. 推定
10. 仮説検定