極座標と極方程式をわかりやすく解説｜スライドで学ぶ高校数学

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学Ⅲ　第5章　2次曲線

	スライド	ノート	問題
1. 放物線
2. 楕円
3. 双曲線
4. 2次曲線の平行移動
5. 2次曲線と直線
6. 2次曲線の性質
7. 曲線の媒介変数表示
8. 極座標と極方程式

8．極座標と極方程式

8.1 極座標

新しい座標の表し方

　これまで平面上の点は，原点と呼ばれる定点Oを通り，その原点で直交する2直線 $x$ 軸， $y$ 軸に垂線を下ろすことによって $(x, y)$ などと表され，これを直交座標と呼んだ．これによって例えば点P $(1, 1)$ と言えば，原点Oから $x$ 軸方向に1， $y$ 軸方向に1だけ移動した点がPであるとわかる．
　ここでは平面上の点を別な方法によって表すことを考える．と言ってもそのアイデアの源流は，既に一般角の三角関数を導入するときに見たものである．

　点P $(1, 1)$ を引き続き例にとると，新しい座標の表し方では，原点からの距離 $\sqrt{2}$ と， $x$ 軸の正の向きとのなす角 $\frac{π}{4}$ によって，P $(\sqrt{2}, \frac{π}{4})$ と表そうというのだ．

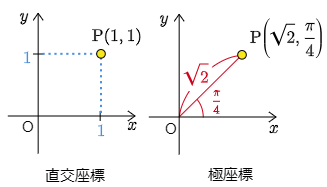
極座標とは

　平面上の点Pの位置を表すのに，極と呼ばれる定点Oからの距離 $r$ と，Oから延びる半直線(始線)からの回転角(偏角) $θ$ によって $(r, θ)$ と表されたものを極座標という．尚，回転角は正の数で反時計回りを，負の数で時計回りをそれぞれ表す．

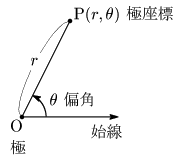
　これによって例えば点P $(2, \frac{π}{3})$ と言えば，極Oからの距離が2で，始線からの回転角が $\frac{π}{3}$ である点だととわかる．

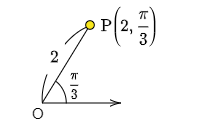
注意

$θ$ は弧度法を用いる．
極Oの極座標は，偏角が定まらないので $θ$ を任意の実数として $(0, θ)$ と定める．
$(r, θ)$ と $(r, θ + 2 n π)$ ( $n$ は整数)は同じ点を表す．

8.2 極座標と直交座標

極座標と直交座標の対応は実にシンプル

　これまでの座標表示(直交座標という) $(x, y)$ と，極座標 $(r, θ)$ との関係は，原点を極， $x$ 軸の正の部分を始線とすると次のようになる：

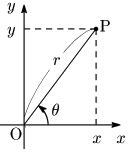
\begin{aligned} x = r \cos θ, y = r \sin θ \\ r^{2} = x^{2} + y^{2} \end{aligned}

例題1　極座標が $(4, \frac{π}{6})$ である点Pの直交座標を求めよ．

こたえ

　解答例を表示する

　 $x = 4 \cos \frac{π}{6} = 2 \sqrt{3}, y = 4 \sin \frac{π}{6} = 2$
　従って　 $(2 \sqrt{3}, 2)$

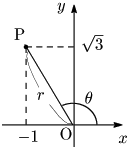
例題2　直交座標が $(- 1, \sqrt{3})$ である点Pの極座標 $(r, θ)$ を求めよ．ただし， $0 ≦ θ < 2 π$ とする．

こたえ

　解答例を表示する

　 $r = \sqrt{(- 1)^{2} + (\sqrt{3})^{2}} = 2$
　また図より　 $θ = \frac{2}{3} π$
　よって　　 $(2, \frac{2}{3} π)$

8.3 極方程式

極方程式とは

　極座標 $(r, θ)$ に関する方程式 $r = f (θ)$ や， $F (r, θ) = 0$ を，極方程式という．例えば $r = 2$ や $r \cos θ = 5$ といった方程式のことであり，これらの方程式が表す図形，すなわちグラフも存在する．私たちがこれまで慣れ親しんできた $y = x + 1$ や $y = x^{2}$ といった方程式と違って，極方程式が表す図形がどういうものなのかを判断するには慣れと経験がそれなりに必要である．また次に示す $r < 0$ の取り扱いが，極方程式の理解を難しくしている．

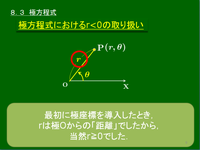
●重要　極方程式における $r < 0$ の取り扱い

　一般に， $\cos (θ + π) = - \cos θ$ ， $\sin (θ + π) = - \sin θ$ であるから，

$\begin{aligned} x = \underset{―}{- r} \cos \underset{―}{θ} = \underset{―}{r} \cos (\underset{―}{θ + π}) \\ y = \underset{―}{- r} \sin \underset{―}{θ} = \underset{―}{r} \sin (\underset{―}{θ + π}) \end{aligned}$

　よって，極方程式においては $r < 0$ も許し，2点 $(- r, θ)$ と $(r, θ + π)$ を同じ点とみなす．

極方程式における $r < 0$ 　点 $(- r, θ)$ は，点 $(r, θ + π)$ とみなす

　極方程式の例として，次の2つの円を考えてみよう．

例1　極Oを中心とする半径1の円の極方程式

　　　 $r = 1$ で， $θ$ は任意

　　よって極方程式は， $r = 1$
　　(極からの距離が1である点の集合)

例2　中心Aの極座標 $(a, 0)$ ，半径 $a$ の円の極方程式

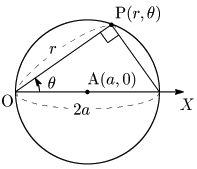
　Pが点Oや点 $(2 a, 0)$ でなければ，円周角の定理により直径の両端と結んでできる∠Pが常に90°であるから，図の三角形は直角三角形である．すると $r$ と $θ$ には常に

$r = 2 a \cos θ$

という関係がある．これはPが点Oや点 $(2 a, 0)$ でも成り立つ．これがこの円の極方程式である．

　 $a = 1$ の場合，すなわち極座標 $(1, 0)$ を中心とする半径1の円について， $P (r, θ)$ の軌跡を次のアニメーションで確認しておこう．

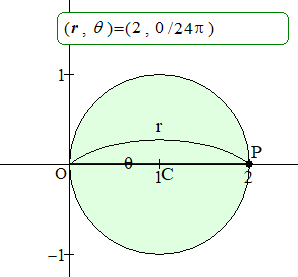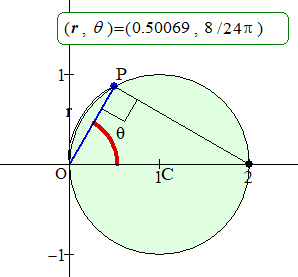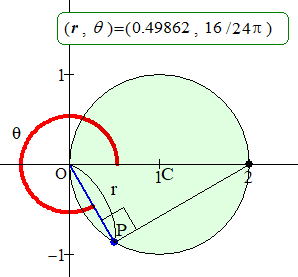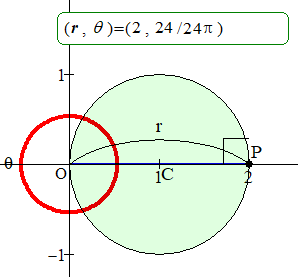
**アニメーション**
( $a = 1$ の場合，すなわち $r = 2 \cos θ$ )
$θ$ が $\frac{12 π}{24} = \frac{π}{2}$ を越えると， $r$ が負になるため，
点を取るときは $r$ を正にし，偏角は $θ + π$ としている．
$\frac{π}{2}$ から急に偏角が大きくなっているのはそのためである．

　上の例からわかるように，ひと口に円といっても，極方程式 $r = 1$ くらいならすぐにその図形のイメージがわくが， $r = 2 \cos θ$ だとどんな図形を表しているのかすぐにはわかりにくい．極方程式の作り方には独特の思考法が要求され，慣れと訓練が必要であるが，円と直線くらいなら程なくして慣れるであろう．

　しかし例え慣れてきたとしても、何せ登場回数が少ない極方程式である．しばらくこの分野から離れようものならすぐに忘れてしまいがちである．私たちは直交座標の方程式ならかなり複雑なものまで理解しているし，極方程式とこれまでの直交座標の方程式は相互に変換が容易なのであるから，極方程式は一旦直交座標の方程式に変換してから考えるのが無難なのかもしれない．

補足1

　 $r < 0$ を許したことで，極方程式の表現が簡素となるメリットがあるものの，図形的な考察に混乱が生じるというデメリットもある．詳しくは 高校数学ワンポイント極方程式における $r$ の正負について 参照．

補足2

　上の例からもわかるように，円を右側に1だけ平行移動しただけなのに，極方程式は全く異なった様相を呈している．極座標，及び極座標を元に成り立つ極方程式においては，平行移動は苦手である．その一方で，拡大・縮小と回転移動は得意としている．

代表的な極方程式

パッと見ただけでは図形がわかりにくいものもある

　以下に身近な図形の極方程式を与える．

直交座標	極座標
$x^{2} + y^{2} = 1$	$r = 1$
$y = x$	$θ = \frac{π}{4}$
$x = 1$	$r \cos θ = 1$
$y = 1$	$r \sin θ = 1$
$(x - a)^{2} + y^{2} = a^{2}$	$r = 2 a \cos θ$
$x^{2} + (y - b)^{2} = b^{2}$	$r = 2 b \sin θ$

例題1　次の極方程式表される曲線は何か．
(1) $r = 6 \cos θ$
(2) $θ = \frac{π}{3}$
(3) $r \cos (θ - \frac{π}{4}) = 2$

こたえ

　解答例を表示する

(1)　 $r = 2 \cdot 3 \cos θ$ より，極座標 $(3, 0)$ を中心とする半径3の円．

(2)　極を通り，始線とのなす角が $\frac{π}{3}$ の直線．

(3)　極座標 $(2, \frac{π}{4})$ を点Aとすると，Aを通り，OAに垂直な直線．

例題2[極方程式→直交座標の方程式]
　極方程式 $r = 2 (\cos θ + \sin θ)$ の表す曲線を，直交座標の方程式で表せ．

こたえ

　解答例を表示する

ポイント 直交座標から極座標への変換 $\begin{array}{ccc} r^{2} & \to & x^{2} + y^{2} \\ r \cos θ & \to & x \\ r \sin θ & \to & y \end{array}$

　与式の両辺に $r$ を掛けて

$r^{2} = 2 (r \cos θ + r \sin θ)$

　 $r^{2} = x^{2} + y^{2}, r \cos θ = x, r \sin θ = y$ を代入して

　 $x^{2} + y^{2} = 2 (x + y)$

故に求める方程式は， $x^{2} + y^{2} - 2 x - 2 y = 0$

例題3[直交座標の方程式→極方程式]
　双曲線 $x^{2} - y^{2} = 1$ を極方程式で表せ．

こたえ

　解答例を表示する

ポイント 極座標から直交座標への変換 $\begin{array}{ccc} x & \to & r \cos θ \\ y & \to & r \sin θ \\ (x^{2} + y^{2} & \to & r^{2}) \end{array}$

　 $x = r \cos θ, y = r \sin θ$ を代入して，

$r^{2} (\cos^{2} θ - \sin^{2} θ) = 1$

$∴ r^{2} \cos 2 θ = 1$

8.4 2次曲線の極方程式

極方程式だと2次曲線は3つまとめて1つの式で表される

　これまでにいくつかの図形の極方程式を見てきたが，次に2次曲線(放物線・楕円・双曲線)の極方程式を確認していこう．直交座標において，これらの方程式は

　　放物線： $y^{2} = 4 p x$
　　楕円　： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
　　双曲線： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$
とそれぞれ異なった形をとっていた．ところがこれらを極方程式で表すと，どれも同じ式になってしまうのである．その原因は，2次曲線の性質 のところで確認したように，離心率 $e$ というものを導入することで，放物線・楕円・双曲線が同じ定義で表現できたというところにある．離心率 $e$ の値によって，放物線・楕円・双曲線のいずれかになるのである．

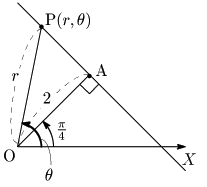
　これから導こうとしている2次曲線の極方程式は，次のような設定である：

2次曲線の極方程式の設定

　焦点：極O
　準線：極座標A $(a, 0) (a > 0)$ を通り，OXに垂直な直線
　離心率： $e$

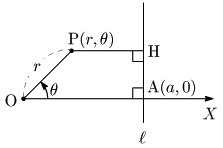
　 $O P : P H = e : 1$ より， $O P = e P H$

　よって

$\begin{aligned} | r | & = e | a - r \cos θ | \\ ∴ r & = \pm e (a - r \cos θ) \end{aligned}$

　 $r$ を含む項を左辺へ，それ以外を右辺に移項して

　　 $(1 + e \cos θ) r = e a$ 　または　 $- (1 - e \cos θ) r = e a$

1°　 $(1 + e \cos θ) r = e a$ のとき，

$r = \frac{e a}{1 + e \cos θ}$ …①

2°　 $- (1 - e \cos θ) r = e a$ のとき，

$\begin{aligned} - r & = \frac{e a}{1 - e \cos θ} \\ ∴ - r & = \frac{e a}{1 + e \cos (θ + π)} \dots ② \end{aligned}$

　①，②を比較すると，

□ $= \frac{e a}{1 + e \cos △}$

という式に，①は $(, △) = (r, θ)$ を，②は $(, △) = (- r, θ + π)$ を代入した式となっている．極方程式のおいては2点 $(r, θ)$ と $(- r, θ + π)$ は同じ点を表すのであったから，①と②は全く同じ曲線を表す式である．従って，①だけで用が足りる．

　2次曲線の性質 のところで確認したように，離心率 $e$ によってこの極方程式は次を表す．
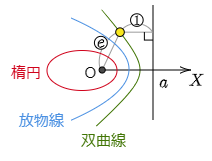
　　 $0 < e < 1$ のとき　楕円
　　 $e = 1$ のとき　　放物線
　　 $e > 1$ のとき　　双曲線

2次曲線の極方程式　焦点が極O，準線が点 $(a, 0) (a > 0)$ を通り，始線OXに垂直な直線，離心率が $e$ である2次曲線の極方程式は $r = \frac{e a}{1 + e \cos θ}$ 　　 $0 < e < 1$ のとき　楕円
　　 $e = 1$ のとき　　放物線
　　 $e > 1$ のとき　　双曲線

例題　極方程式 $r = \frac{3}{1 + 2 \cos θ}$ を直交座標の方程式で表せ．

こたえ

　解答例を表示する

　与式を変形して　 $r (1 + 2 \cos θ) = 3$

$∴ r = 3 - 2 r \cos θ$

　 $r \cos θ = x$ であるから， $r = 3 - 2 x$

　両辺を2乗して　 $r^{2} = (3 - 2 x)^{2}$

　 $r^{2} = x^{2} + y^{2}$ を代入して，

$\begin{aligned} x^{2} + y^{2} & = 9 - 12 x + 4 x^{2} \\ 3 (x - 2)^{2} - y^{2} & = 3 \\ (x - 2)^{2} - \frac{y^{2}}{3} & = 1 \end{aligned}$

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学Ⅲ　第5章　2次曲線

	スライド	ノート	問題
1. 放物線
2. 楕円
3. 双曲線
4. 2次曲線の平行移動
5. 2次曲線と直線
6. 2次曲線の性質
7. 曲線の媒介変数表示
8. 極座標と極方程式

8．極座標と極方程式【ノート】1人で学べる！高校数学

8．極座標と極方程式

8.1 極座標

新しい座標の表し方

極座標とは

注意

8.2 極座標と直交座標

極座標と直交座標の対応は実にシンプル

8.3 極方程式

極方程式とは

●重要 極方程式における r<0 の取り扱い

補足1

補足2

代表的な極方程式

パッと見ただけでは図形がわかりにくいものもある

8.4 2次曲線の極方程式

極方程式だと2次曲線は3つまとめて1つの式で表される

2次曲線の極方程式の設定

8．極座標と極方程式【ノート】
1人で学べる！高校数学

●重要　極方程式における $r < 0$ の取り扱い