高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |

5.2次曲線と直線
5.1 2次曲線と直線の共有点
共有点の個数を求める際の考え方は,これまでと何ら変わらない
2次曲線と直線の共有点を考察するにあたって,これまでにない何か特別なことがある訳ではない.基本的には x か y のどちらかの文字を消去して2次方程式を作り,その解の種類,個数を考察するのである.しかし楕円に関しては,下の例題にある通り楕円と円の親戚関係を利用することで,計算が大幅にラクになる場合がある.
直線との共有点の個数の求め方放物線:連立して判別式
楕 円:連立して判別式
双曲線:直線と漸近線が平行でない
→放物線・楕円の-ケースと同じ
直線と漸近線が平行
→漸近線そのもの→0個
→それ以外→1個
例題1 双曲線 x212−y23=1 と直線 y=x+k の共有点の個数を求めよ.
こたえ
補足
D=0 のとき,接するという.漸近線に平行な直線は接線になり得ない.
楕円の場合は円との親戚関係を用いた上手い考え方がある
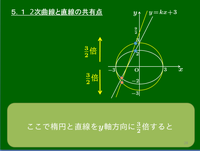
例題2 楕円 x29+y24=1 と直線 y=kx+3 の共有点の個数を求めよ.
方針
例題1と同様に解決できるが,楕円と円の関係を用いた次の解法がおすすめ.
こたえ

5.2 2次曲線の接線の方程式
2次曲線上の点における接線の方程式には公式がある
2次曲線上の点 (x1, y1) 上における接線の方程式は次で与えられる:
2次曲線の接線の方程式
接点の座標が (x1,y1) のとき,
①放物線 y2=4px→y1y=2p(x+x1)
②楕円 x2a2+y2b2=1→x1xa2+y1yb2=1
③双曲線 {x2a2−y2b2=1→x1xa2−y1yb2=1x2a2−y2b2=−1→x1xa2−y1yb2=−1
覚え方
①放物線 2x→x+x1, y2→y1y
②③楕円,双曲線 x2→x1x, y2→y1y
証明
数学Ⅲの微分法を用いる証明が最もはやいが,それでなければ次の方法が明快.
点 (x1,y1) を通り,方向ベクトルが (α,β) である直線 ℓ のベクトル方程式は,t を実数として(x,y)=(x1,y1)+t(α,β)∴{x=x1+αty=y1+βt ⋯(∗)と表せる.この直線が2次曲線上の点 (x1, y1) における接線となるとき,x,y を消去して得られる t の2次方程式が \boldsymbol{t=0} を重解にもつ.(さもなくば,t=0 以外の t に対応する点で,2次曲線と直線が共有点をもち,接していないことになる.)
① 放物線
y^2=4px に (*) を代入して,
\begin{align} (y_1+\beta t)^2&=4p(x_1+\alpha t)\\[5pt] {y_1}^2+2y_1\beta t+\beta^2t^2&=4px_1+4p\alpha t\\[5pt] \end{align}
{y_1}^2=4px_1 に注意して整理すると,
\beta^2t^2-2(2p\alpha-y_1\beta)t=0 …①
2次の係数 \beta^2 について,\beta=0 とすると,直線の方向ベクトルが (\alpha,\ 0) となり,直線は x 軸と平行になるが,放物線 y^2=4px の接線にそのようなものはないので \beta\neq0 である.よって①は t の2次方程式である.\ell が放物線の接線のとき,この2次方程式が t=0 を重解にもつから,
\begin{align} 2p\alpha-y_1\beta&=0\\[5pt] \therefore (2p,-y_1)\cdot(\alpha,\beta)&=0 \end{align} 従ってベクトル (2p,\ -y_1) は,\ell の方向ベクトル (\alpha,\beta) と垂直であるから,\ell の法線ベクトルとなる.よって,接線の方程式は,\begin{align} 2p(x-x_1)-y_1(y-y_1)&=0\\[5pt] 2\,p\,x-2\,p\,x_1-y_1\,y+y_1^2&=0\end{align}
{y_1}^2=4px_1 であるから2\,p\,x-2\,p\,x_1-y_1y+4\,p\,x_1=0\therefore y_1y=2p(x+x_1)
②,③ 楕円,双曲線
曲線 C の方程式を,p>0,q\neq0 として
C:p\,x^2+q\,y^2=1
とおく.q>0 のときは楕円で,q<0 のときは双曲線を表す.C 上の点を (x_1,y_1) とし,(*) を代入すると,
p(x_1+\alpha t)^2+q(y_1+\beta t)^2 =1
展開して t について整理すると,p{x_1}^2+q{y_1}^2=1 にも注意して
(p\alpha^2+q\beta^2)t^2+2(p\,\alpha\, x_1+q\,\beta \,y_1)t =0
t^2 の係数 p\,\alpha^2+q\,\beta^2 について,これが0でないことを確認しておこう.(\alpha,\ \beta) は \ell の方向ベクトルだからもちろん (\alpha,\ \beta)\neq\overrightarrow0.p>0 と仮定しておいたから, q>0 のときは p\,\alpha^2+q\,\beta^2\neq0.また q<0 の場合でも,p\,\alpha^2+q\,\beta^2=0 となるときは,\ell の方向ベクトル (\alpha,\ \beta) が双曲線の漸近線の方向ベクトル (\sqrt{-q},\ \pm\sqrt{p}) と平行になってしまうから不適.以上により p\,\alpha^2+q\,\beta^2\neq0 であることがわかった.
よって \ell が2次曲線の接線のとき,この t の2次方程式が t=0 を重解にもつから,
\begin{align} p\,\alpha\, x_1+q\,\beta\, y_1&=0\\[5pt] (\alpha,\ \beta)\cdot(p\,x_1,\ q\,y_1)&=0 \end{align}
よって,(\alpha,\ \beta)\perp(p\,x_1,\ q\,y_1) であるから,ベクトル (p\,x_1,\ q\,y_1) は接線の法線ベクトルとなる.
ベクトル (p\,x_1,\ q\,y_1) について,これが \overrightarrow0 でないことを確認しておこう.p>0 であるから x_1\neq0 のときは (p\,x_1,\ q\,y_1)\neq\overrightarrow0.また,x_1=0 のときは p\,{x_1}^2+q\,{y_1}^2=1 から y_1\neq0 だから,このときも (p\,x_1,\ q\,y_1)\neq\overrightarrow0.以上により,(p\,x_1,\ q\,y_1)\neq\overrightarrow0 であることがわかった.
従って接線の方程式は,
p\,x_1(x-x_1)+q\,y_1(y-y_1)=0
整理して,p{x_1}^2+q{y_1}^2=1 を用いると,
px_1x+qy_1y=1
補足
数学Ⅲの微分が使えれば,その場での導出もたやすい
数学Ⅲの微分法を用いると次のように示される:
① 放物線
y^2=4px の両辺を x で微分して 2yy’=4p
y\neq0 のとき,y’=\dfrac{2p}y.
従ってこのとき接線の方程式は,
\begin{align} y-y_1&=\frac{2p}{y_1}(x-x_1)\\[5pt] \therefore y_1y&=2p(x-x_1)+{y_1}^2\\[5pt] \therefore y_1y&=2p(x+x_1)\ \ (\because {y_1}^2=4px_1)\\[5pt] \end{align}
頂点 (0,0) における接線の方程式は x=0 であるが,上の式で (x_1,y_1)=(0,0) とおくと x=0 となるから,上の式はこの場合も含まれる.
② 楕円
楕円 \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 の両辺を x で微分して\frac{2x}{a^2}+\frac{2yy’}{b^2}=0 y\neq0 のとき y’=-\dfrac{b^2x}{a^2y}
従ってこのとき接線の方程式は,y-y_1=-\dfrac{b^2x_1}{a^2y_1}(x-x_1)
両辺を \dfrac{y_1}{b^2} 倍して
\begin{align} \frac{y_1y}{b^2}-\frac{{y_1}^2}{b^2}&=-\frac{x_1}{a^2}(x-x_1)\\[5pt] \therefore \frac{x_1x}{a^2}+\frac{y_1y}{b^2}&=1\ \ (\because \frac{{x_1}^2}{a^2}+\frac{{y_1}^2}{b^2}=1) \end{align}
(x_1,y_1)=(\pm a,0) における接線の方程式は x=\pm a (複号同順)だから,上の式はこの場合も含まれる.
③ 双曲線
②の楕円の場合と同様にして示される.

例題 点 (0,3) から楕円 x^2+4y^2=4 に引いた接線の方程式,及び接点の座標を求めよ.
こたえ

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |