高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |

3.双曲線
実は双曲線の登場はここが初めてではない.これまでにも反比例の式として双曲線 y=1x が出てきていた.放物線のときと同様に,双曲線も2次曲線という枠組みの中での定義がどうなっているかを確認していこう.
3.1 双曲線の方程式
2次曲線における双曲線とは
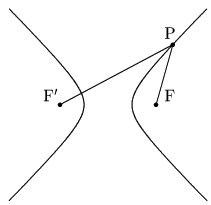
2定点F,F’からの距離の差が一定である点Pの軌跡
2定点F,F’を焦点という.

双曲線の方程式
双曲線の方程式の導出法
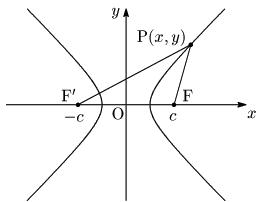
焦点:F(c,0),F’(−c,0)
距離の差:2a (ただし,c>a>0)
である双曲線の方程式を求める.
|FP−F′P|=2a ⋯①⟺FP−F′P=±2a⟺FP=F′P±2a⟹ FP2=(F′P±2a)2⟺FP2=F′P2±4a⋅F′P+4a2⟺(x−c)2+y2=(x+c)2+y2±4a√(x+c)2+y2+4a2⟺±a√(x+c)2+y2=a2+cx⟺a2{(x+c)2+y2}=(a2+cx)2⟺(c2−a2)x2−a2y2=a2(c2−a2)
ここで √c2−a2=b とおくと,
b2x2−a2y2=a2b2∴ x2a2−y2b2=1 ⋯②
よって条件①を満たす点は,曲線②上にある.逆に曲線②上の任意の点は,c=√a2+b2 とおくことで条件①を満たす.(詳しくはスライド で.)
方程式②を,双曲線の方程式の標準形という.
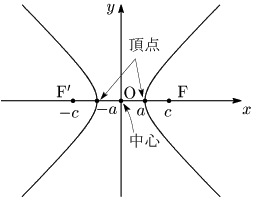
直線FF’と双曲線の2つの交点を頂点,線分FF’の中点を双曲線の中心という.
双曲線は,x 軸,y 軸,原点に関して対称である.
補足
双曲線においては,a,b の大小関係を考えなくてよい.
発展的補足
双曲線上の任意の点から焦点までの距離は,ルートがつかない
平面上の2点 (x1, y1), (x2, y2) の距離は,√(x1−x2)2+(y1−y2)2 で計算され,通常ルート √ は外れないことが多い.しかし,放物線 や 楕円 のときがそうであったように,双曲線の場合も双曲線上の任意の点と,一方の焦点までの距離は,ルートがつかない式として表すことができるのである.
双曲線上の任意の点を (x1, y1) とする.x12a2−y12b2=1 より y12=b2(x12a2−1) であることに注意すると,例えば焦点 (c, 0) までの距離は,
√(x1−c)2+y12=√(x12−2cx1+c2)+y12=√(x12−2cx1+c2)+b2(x12a2−1)=√a2+b2a2x12−2cx1−b2+c2=√c2a2x12−2cx1+a2 (∵ c=√a2+b2)=√(cax1−a)2=|cax1−a|
と表される.すなわち双曲線上の任意の点 (x1, y1) と焦点 (c, 0) までの距離 √(x1−c)2+y12 は,|cax1−a| としてルートがつかない式で表されるのである.もう一方の焦点 (−c, 0) までの距離は,この式の c を −c に置き換えればよい.
焦点からの距離が最も小さい点は頂点
ついでに述べておくと,この式によって,焦点 (c, 0) からの距離が最小となる双曲線上の点は,頂点の1つである点 (a, 0) で,その最小値は c−a であることがわかる.何故なら,関数 y=|cax−a| のグラフが次のようになるからである.
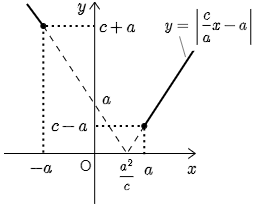
これで放物線,楕円,双曲線の各場合について,曲線上の任意の点から焦点までの距離がルートを含まない式として表すことができることを見た.この事実は難関大入試問題で,曲線上の2点と焦点を結んだ三角形を考えさせる問題などで活躍する場合がある.
双曲線の漸近線
漸近線の方程式の求め方
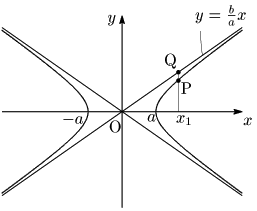
x2a2−y2b2=1 ⋯①より
y2=b2a2(x2−a2)
今,x>0,y>0 の場合を考えると,
y=ba√x2−a2
となる.ここで,直線 y=bax との差(図のPQ)を考えると,
PQ=bax1−ba√x12−a2=ba(x1−√x12−a2)=ba⋅(x1−√x12−a2)(x1+√x12−a2)(x1+√x12−a2)=ba⋅a2(x1+√x12−a2)=ab(x1+√x12−a2)→0 (x1→∞)
となるから,第1象限で y=bax は漸近線となる.
①は原点に関して対称であるから,y=bax は第3象限でにおいても漸近線である.
また,①は y 軸に関しても対称であるから,y=−bax も①の漸近線である.
双曲線の性質 双曲線 x2a2−y2b2=1 (a>0, b>0) において,
- 焦点は x 軸上で,F(√a2+b2,0),F’(−√a2+b2,0)
中心(線分 FF′ の中点)は 点 (0,0) - 座標軸との交点(頂点)は (a,0), (−a,0)
- x 軸,y 軸,原点に関して対称
- 漸近線は,2直線 xa−yb=0, xa+yb=0
- 楕円上の任意の点から焦点までの距離の差は 2a
補足1
漸近線の覚え方
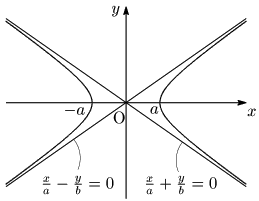
漸近線の方程式は,双曲線 x2a2−y2b2=1 の右辺を0とおいた,x2a2−y2b2=0,即ち
(xa+yb)(xa−yb)=0
の表す2直線である.
補足2
c=√a2+b2 の覚え方
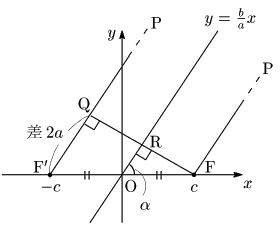
双曲線 x2a2−y2b2=1 の焦点の x 座標 c が c=√a2+b2 となることを,漸近線の方程式から幾何的考察を行うことで求める方法を紹介する.
双曲線上の点Pが第1象限の無限遠方にある場合は,下図でほぼ PF//PF′ となるから,焦点までの距離の差が F′Q=2a より OR=12F′Q=a.また,tanα=ba より,FR=ORtanα=b.よって,△OFRにおいて,c=√a2+b2.
補足3
直角双曲線とは
直交する漸近線をもつ双曲線を,直角双曲線という.中学生の時に学んだ反比例の式 y=1x のグラフも直角双曲線である.
例 x2−y2=1 (漸近線:x±y=0)

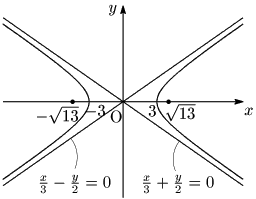
例題 双曲線 x29−y24=1 の焦点,頂点,漸近線の方程式を求め,グラフをかけ.漸近線もかくこと.
こたえ
焦点:√9+4=√13 より,(√13,0),(−√13,0)
頂点:(3,0),(−3,0)
漸近線:x3−y2=0,x3+y2=0

3.2 焦点が y 軸上にある双曲線
焦点が y 軸上にあるときは y=x に関する対称移動で考える
曲線 x2a2−y2b2=−1 (a>0,b>0) ⋯① を,直線 y=x に関して対称移動すると,
y2a2−x2b2=−1 ∴x2b2−y2a2=1
これは双曲線の方程式で,
焦点 :F(√a2+b2,0),F’(−√a2+b2,0)
頂点 :(b,0), (−b,0)
漸近線:xb−ya=0, xb+ya=0
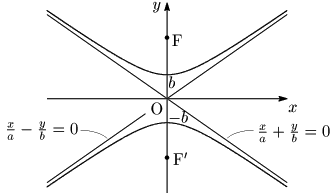
であったから,対称移動前を考えると①は次のような双曲線であることがわかる:
焦点 :F(0,√a2+b2),F’(0,−√a2+b2)
頂点 :(0,b), (0,−b)
漸近線:xa−yb=0, xa+yb=0
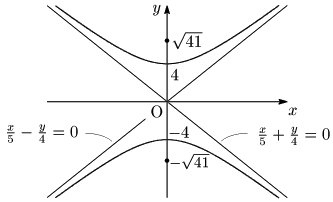
例題 双曲線 x225−y216=−1 の焦点,頂点,漸近線を求め,グラフをかけ.漸近線もかくこと.
こたえ
焦点:√25+16=√41 より,(0,√41),(0,−√41)
頂点:(0,4),(0,−4)
漸近線:x5−y4=0,x5+y4=0

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |