円と2直線に関する定理として,方べきの定理と呼ばれるものがあり,円と直線を絡めた問題ではしばしばこの定理を使って線分の長さを計算します.また,この定理も逆命題が成り立ち,「方べきの定理の逆」と呼ばれています.ここではこれらの定理の証明を丁寧に説明していきます.
高校数学[総目次]
数学A 第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [会員] | [会員] | |
| 2. メネラウスの定理 | [会員] | [会員] | |
| 3. チェバの定理の逆 | [会員] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |

| 7.1 方べきの定理 | スライド① |
| 7.1 方べきの定理(続き) | スライド② |
| 7.2 方べきの定理の逆 | スライド③ |
| 7.2 方べきの定理の逆(続き) | スライド④ |
スライドはぜひ全画面表示で
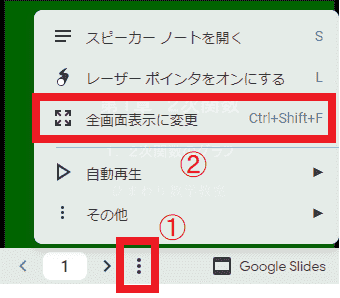
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
