関数の連続性を主張するための3つの事柄を確認します.
次に連続性に関する性質を見ます.
関数の連続性は「で」連続といったように,各の値において決まるものですが,定義域全体で連続である関数を連続関数といいます.
閉区間で定義された連続関数には必ず最小値と最大値が存在します.
高校数学[総目次]
数学Ⅲ 第1章 極限
| スライド | ノート | 問題 | |
| 1. 数列の極限 | [無料] | ||
| 2. 無限等比数列 | [無料] | ||
| 3. 無限級数 | [会員] | [会員] | |
| 4. 無限等比級数 | [会員] | ||
| 5. 関数の極限 | [会員] | ||
| 6. (sin x)/x の極限 | [会員] | ||
| 7. 関数の連続性 | [会員] |
| 7.1 関数が連続であるための条件 | スライド① |
| 7.2 連続性の性質 7.3 連続関数 7.4 区間で連続 7.5 連続関数の最大値・最小値の定理 |
スライド② |
スライドはぜひ全画面表示で
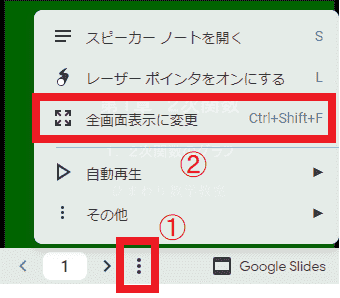
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
