2次方程式の2つの解について,それらの和と積は,元の方程式の係数と密接な関係があり,「解と係数の関係」と呼ばれています.これは大変に重要です.
2次方程式の2解をα,βα,βとすると,α+β,αβα+β,αβ の2式は,ααとββに関する対称式における基本対称式です.どんな対称式も基本対称式だけを使って書けるため,多くの場面で解と係数の関係が利用されます.
高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | [会員] | |
| 2. 2次方程式の解と判別式 | [会員] | |
| 3. 解と係数の関係 | [会員] | |
| 4. 剰余の定理・因数定理 | [会員] | |
| 5. 高次方程式 | [会員] |

| 3.1 解と係数の関係 | スライド① |
| 3.2 2次式の因数分解 | スライド② |
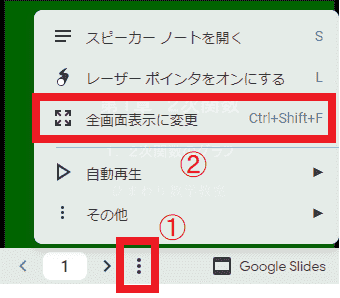
スライドはぜひ全画面表示で
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
