三角形の各辺と,それに対応する角は3組あります.これら3組の辺の長さと,対応する角のsin(正弦)との比の値は一定となります.そして,その比の値は三角形の外接円の直径と等しくなります.これを正弦定理といいます.
この節では,正弦定理とその証明,及び例題をみていきましょう.
高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [会員] | [会員] | |
| 2. 三角比の相互関係 | [会員] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |

4.正弦定理
| 4.1 辺の長さと正弦 | スライド① |
| 4.2 正弦定理 | スライド② |
スライドはぜひ全画面表示で
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
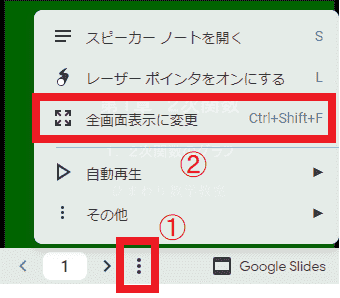
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
