三角比を90°以上180°以下の角に拡張するため,三角比を定義し直します.その際,90度未満で直角三角形を用いていた定義が,そのまま内包され,90°以上ではその自然な拡張となるように定義します.
次に,単位円によって拡張された三角比を確認します.この単位円による三角比の見方がとりわけ重要です.何故というに,三角比の値を目に見える形で捉えることができるからです.これ以降の三角比はこの単位円による考え方がメインとなります.
続いて,0°から180°までの三角比がとりうる値の範囲,及び符号を確認します.
180°-θの三角比を見たのち,三角比を含む等式の解法を学習します.
これまでに出てきた三角比の相互関係は,0°以上180°以下の新しい三角比の定義の下でもそのまま成り立ちます.
高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [会員] | [会員] | |
| 2. 三角比の相互関係 | [会員] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |

3.三角比の拡張
| 3.1 座標を用いた三角比の定義 | スライド① |
| 3.2 単位円における三角比 | スライド② |
| 3.3 180° – θ の三角比 | スライド③ |
| 3.4 等式を満たす θ | スライド④ |
| 3.5 三角比の相互関係 | スライド⑤ |
スライドはぜひ全画面表示で
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
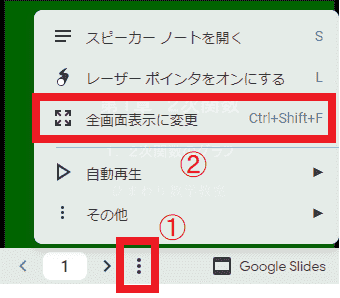
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
